kosaraju算法求解强连通分量
kosaraju算法通过对一个有向图的正图和反图两次DFS,从而求解出该有向图的所有强连通分量。
对于无向图连通分量的求解,只需要通过一次对原图的DFS搜索便可以很好的解决,但同样的问题放到有向图身上,就有一点麻烦了,以下面的这个有向图的强连通分量的求解为例:
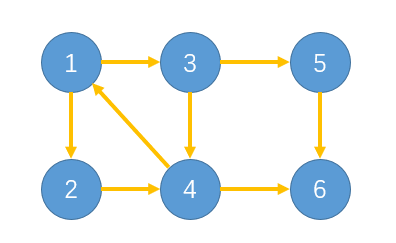
如果只是简单的在原图上进行DFS的话,可以发现,DFS搜索的时候会横跨两个强连通分量,导致我们无法区分搜索得到的结点是否属于同一个强连通分量。kosaraju算法的想法是,将每一个强连通分量看成是一个大的结点,这样之后,整张图就变成一个有向无环图了,并且在这个DAG中的每条边均是从一个强连通分量指向另一个强连通分量。
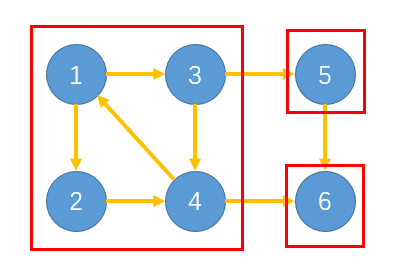
并且,在原图中,若存在边(u,v),即有一条有向边从强连通分量u指向强连通分量v。那么,u的结束时间会大于v的结束时间;换句话说,每条边总是指向结束时间更小的强连通分量。相应的,在转置G^T中,每条边则总是指向结束时间更大的强连通分量。
那么,选取结束时间最晚的结点,其所对应的强连通分量的结束时间必然是最大的。而在转置G^T中每条边总是指向结束时间更大的强通分量,因为现在考虑的强连通分量已经拥有最大的结束时间,那么就没有从这个强连通分量指向别的强连通分量的边。因此,可以保证对这个选取的顶点做DFS,不会搜索到别的连通分量的顶点。
由此,可得出kosaraju算法的基本流程:
- 对原图进行后序DFS,得到原图的“逆拓扑序”(引号是因为原图中是存在环的,并不存在拓扑排序,当然可以理解成进行缩点之后的连通分量的逆拓扑序)
- 将“逆拓扑序”存入栈中,之后从栈顶依次取出,在原图的反图上按照这个顺序进行DFS
– 从节点1出发,能走到 2 ,3,4 , 所以{1 , 2 , 3 , 4 }是一个强连通分量
– 从节点5出发,无路可走,所以{ 5 }是一个强连通分量
– 从节点6出发,无路可走,所以{ 6 }是一个强连通分量
自此Kosaraju Algorithm完毕,这个算法只需要两遍DFS即可,是一个比较易懂的求强连通分量的算法。
附上一个模板题洛谷B3609以及AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
using namespace std;
vector<vector<int>> edge; //使用邻接表建图
vector<vector<int>> edge_t; //反图
vector<int> visit;
stack<int> s;
bool cmp(vector<int> &x,vector<int>& y)
{
return x[0]<y[0];
}
void dfs(int x)
{
if(visit[x]==1) return;
int t=edge[x].size();
visit[x]=1;
for(int i=0;i<t;i++)
{
dfs(edge[x][i]);
}
s.push(x);
}
void r_dfs(int x,vector<int>& ret)
{
if(visit[x]==1) return;
int t=edge_t[x].size();
visit[x]=1;
ret.emplace_back(x);
for(int i=0;i<t;i++)
{
r_dfs(edge_t[x][i],ret);
}
}
int main()
{
int n,m;
cin>>n>>m;
edge.resize(n);
edge_t.resize(n);
visit.resize(n);
for(int i=0;i<m;i++)
{
int x,y;
cin>>x>>y;
if(x==y) continue;
edge[x-1].emplace_back(y-1);
edge_t[y-1].emplace_back(x-1);
}
for(int i=0;i<n;i++)
{
if(visit[i]==1) continue;
dfs(i);
}
for(int i=0;i<n;i++) visit[i]=0;
vector<vector<int>> ans;
while(s.empty()==false)
{
int t=s.top();
s.pop();
if(visit[t]==0)
{
vector<int> temp;
r_dfs(t,temp);
sort(temp.begin(),temp.end());
ans.emplace_back(temp);
}
}
cout<<ans.size()<<endl;
sort(ans.begin(),ans.end(),cmp);
for(int i=0;i<ans.size();i++)
{
for(int j=0;j<ans[i].size();j++)
{
cout<<ans[i][j]+1<<" ";
}
cout<<endl;
}
return 0;
}
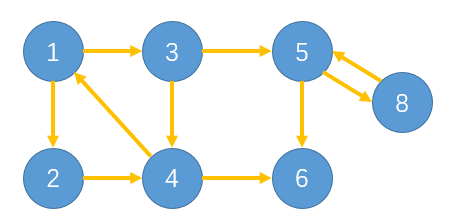
现在考虑按问题中的方式用原图来做第二次深度优先搜索。注意到在原图中,每条边总是指向结束时间更小的强连通分量。 因此,如果我们能找到结束时间最小的强连通分量,并按照结束时间递增的方式来依次进行dfs,也是能得到各个不同的强连通分量的。但问题是,一个顶点的结束时间是最小的,_并不能保证它所对应的强连通分量的结束时间是最小的_。如下图的例子所示,按照搜索路径1->3->5->8,8是最早结束的结点,但是5->8并不是最早结束的强连通分量。
Reference
end☆~