凸包算法

Posted on Edited on

凸包是一个计算几何中的概念，其形式化定义为在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。在二维欧几里得空间中，凸包可想象为将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。

常见的求解二维凸包的算法有很多种，这里只简单介绍一下Andrew算法。
以LeetCode587为例，这道题可以说是一道二维凸包的模板题。

Andrew算法正是用于求解凸包上的所有点（围成所有点的最小周长），其算法逻辑将凸包分为「上凸壳」和「下凸壳」，并分别求出，如下图所示，蓝色分割线将凸包分为两部分：

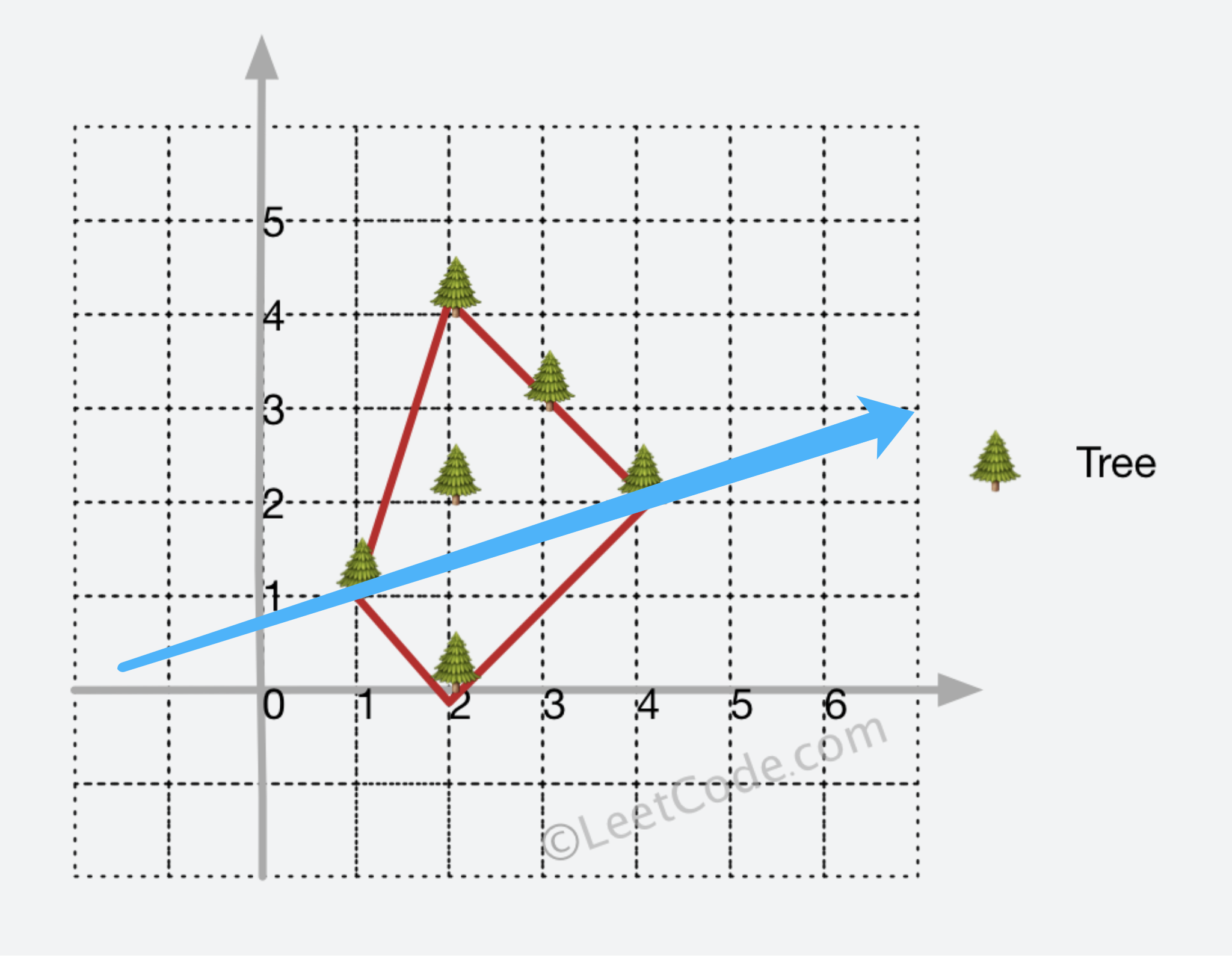
Andrew算法的流程如下：

  • 1. 对所有点进行排序，先根据$x$坐标排升序，后根据$y$坐标排升序;根据$x$排升序的目的，是为了我们能够往一个方向画出凸包边缘（从左往右画出一半凸壳，从右往左画出另外一半），而将$y$升序目的是可以确保一旦我们现在从$a$到$b$进行连线，那么$a$到$b$之间的所有点能够确保被围住;
  • 2. 使用栈来维护所有凸包上的点，或者说凸包上的边，会更为准确，因为凸包起点元素会在栈中出现两次（首尾），因此更为准确的描述应该是使用栈维护凸包的所有的边，栈中相邻元素即代表凸包上的一条边;
  • 3. 分别「从左往右」和「从右往左」处理排序好的所有点，来分别画出凸包的上下两部分，根据画的是第一部分还是第二部分，维护栈内元的处理逻辑稍有不同：
    • 第一部分(上凸壳):
      • 3.1 若栈内元素少于2个，由于组成一条线至少需要两个点，说明此时第一条边都还没画出，直接将元素添加到栈中；
      • 3.2 若栈内元素不少于2个，考虑是否要将栈顶的边删掉（由栈顶前两个元素组成的边）假设栈顶元素为$b$，栈顶元素的下一位为$a$，即栈顶存在一条$a$到$b$的边，当前处理到的点为$c$，此时我们根据$ac$边是否在$ab$边的顺时针方向来决定是否要将$ab$边去掉。
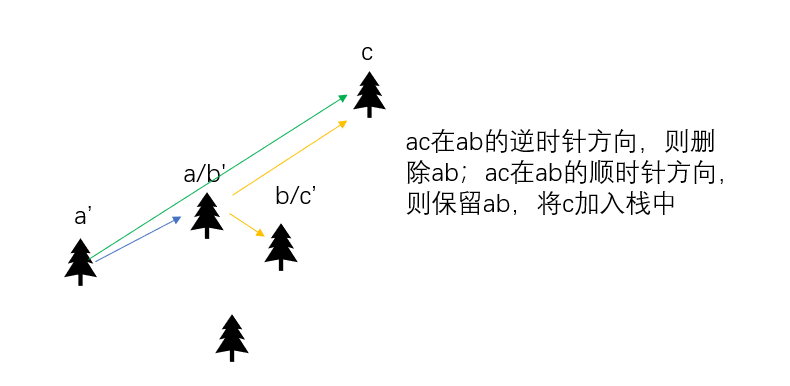
  • 第二部分(下凸壳):
    • 3.3 逻辑同理，唯一需要注意的是，第一部分的凸包边我们不能删去，假定处理完第一部分凸包，我们栈内有$m$个元素，我们需要将上述「栈顶元素不少于2个」的逻辑替换为「栈顶元素大于$m$个」，同时已参与到凸包第一部分的点，不能再考虑，因此需要额外使用一个$vis$数组来记录使用过的点。

为了方便取得栈顶的前两位元素，我们使用数组实现栈。
具体的AC代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
class Solution {
public:
vector<pair<int,int> > points;

pair<int,int> sub(pair<int,int> a,pair<int,int> b)
{
    return make_pair(a.first-b.first,a.second-b.second);
}

double cross(pair<int,int> a,pair<int,int> b)
{
    return a.first*b.second-a.second*b.first;
}

double getarea(pair<int,int> a,pair<int,int> b,pair<int,int> c)
{
    return cross(sub(b,a),sub(c,a));
}

    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
    int n=trees.size();
    for(int i=0;i<n;i++) points.emplace_back(make_pair(trees[i][0],trees[i][1]));
    sort(points.begin(),points.end());
    vector<int> stack(n+10);
    vector<int> vis(n);
    int tp=0; //栈顶指针
    tp++;
    stack[tp]=0;
    //第一轮，寻找上凸壳
    for(int i=1;i<n;i++)
    {
        pair<int,int> c=points[i];
        while(tp>=2)
        {
            pair<int,int> a=points[stack[tp-1]]; //栈顶次元素
            pair<int,int> b=points[stack[tp]];  //栈顶元素
            if(getarea(a,b,c)<0) 
            {
                vis[stack[tp]]=0;
                tp--;
            }
            else break;
        }
        tp++;
        stack[tp]=i;
        vis[i]=1;
    }
    //第二轮，从后往前，寻找下凸壳
    int size=tp;
    for(int i=n-1;i>=0;i--)
    {
        if(vis[i]==1)  continue;
        pair<int,int> c=points[i];
        while(tp>size)
        {
            pair<int,int> a=points[stack[tp-1]];
            pair<int,int> b=points[stack[tp]];
            if(getarea(a,b,c)<0)  tp--;
            else break;
        }
        tp++;
        stack[tp]=i;
    }
    vector<vector<int>> ans;
    for(int i=1;i<tp;i++)  //起始节点可能会在栈中出现两次
    {
        vector<int> temp(2);
        temp[0]=points[stack[i]].first;
        temp[1]=points[stack[i]].second;
        ans.emplace_back(temp);
    }
    return ans;
    }
};

end☆~