A*(A Star)算法是一种很常用的路径查找和图形遍历算法,它可以被认为是Dijkstra算法的扩展。相较于普通的bfs算法,借助启发函数的引导,A*算法通常拥有更好的性能。
既然提到了dij,就先贴一个堆优化的dij的模板,虽然和后续A*算法的模板没什么关系 普通的优先队列,至于什么斐波那契堆就算了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| vector<int> dis;
priority_queue<pair<int,int>> q;
vector<vector<pair<int,int>> > map;
for(int i=0;i<=n;i++)
{
dis.emplace_back(INT_MAX);
}
dis[n]=0;
q.push(make_pair(0,n));
while(q.empty()==false)
{
while(q.empty()==false && (-q.top().first>dis[q.top().second]))
{
q.pop();
}
if(q.empty()==true) break;
int x=q.top().second;
q.pop();
for(int i=0;i<map[x].size();i++)
{
int y=map[x][i].first;
if(dis[y]>dis[x]+map[x][i].second)
{
dis[y]=dis[x]+map[x][i].second;
q.push(make_pair(-dis[y],y));
}
}
}
|
A*算法通过下面这个函数来计算每个节点的优先级,并在运算过程中,每次从优先队列中选取f(n)值最小(优先级最高)的节点作为下一个待遍历的节点,来达到加快搜索的目的。
$$f(n)=g(n)+h(n)$$
其中:
·f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时,我们总会选取综合优先级最高(值最小)的节点。
·g(n) 是节点n距离起点的代价。
·h(n)是节点n距离终点的预计代价,这也就是A*算法的启发函数。
$f(n)=g(n)+h(n)$其实相当于经过结点n的一条预估最短路径的大小。
不难发现,启发函数会影响A*算法的行为,也影响着A*算法的性能。通过调节启发函数我们可以控制算法的速度和精确度。在一些情况,未必需要最短路径,而是希望能够尽快找到一个路径就行。
·在极端情况下,当启发函数h(n)始终为0,则将由g(n)决定节点的优先级,此时算法就退化成了Dijkstra算法。
·如果h(n)始终小于等于节点n到终点的代价,则A*算法保证一定能够找到最短路径。但是当h(n)的值越小,算法将遍历越多的节点,也就导致算法越慢。
·如果h(n)完全等于节点n到终点的代价,则A*算法将找到最佳路径,并且速度很快。可惜的是,并非所有场景下都能做到这一点。因为在没有达到终点之前,我们很难确切算出距离终点还有多远。
·如果h(n)的值比节点n到终点的代价要大,则A*算法不能保证找到最短路径,不过此时会很快。
在另外一个极端情况下,如果h(n)相较于g(n)大很多,则此时只有h(n)产生效果,这也就变成了最佳优先搜索。
具体的模板如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| struct astar
{
static int geth(const string& status,const string& target)
{
...
}
astar(const string& status, const string& target, int g): status_{status}, g_{g}, h_{geth(status, target)} {
f_ = g_ + h_;
}
bool operator< (const astar& that) const {
return f_ > that.f_;
}
string status_;
int f_;
int g_;
int h_;
};
|
有了模板,现在就可以写两道题来练练手了。实际上,A*算法模板本身并没有什么难度,主要的难度在于如何选取合适的启发函数。
leetcode 752. 打开转盘锁[https://leetcode-cn.com/problems/open-the-lock/]
题目描述:
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转:例如把 ‘9’ 变为 ‘0’,’0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000’ ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
输入:deadends = [“0201”,”0101”,”0102”,”1212”,”2002”], target = “0202”
输出:6
解释:
可能的移动序列为 “0000” -> “1000” -> “1100” -> “1200” -> “1201” -> “1202” -> “0202”。
注意 “0000” -> “0001” -> “0002” -> “0102” -> “0202” 这样的序列是不能解锁的,
因为当拨动到 “0102” 时这个锁就会被锁定。
示例 2:
输入: deadends = [“8888”], target = “0009”
输出:1
解释:
把最后一位反向旋转一次即可 “0000” -> “0009”。
示例 3:
输入: deadends = [“8887”,”8889”,”8878”,”8898”,”8788”,”8988”,”7888”,”9888”], target = “8888”
输出:-1
解释:
无法旋转到目标数字且不被锁定。
示例 4:
输入: deadends = [“0000”], target = “8888”
输出:-1
提示:
·1 <= deadends.length <= 500
·deadends[i].length == 4
·target.length == 4
·target 不在 deadends 之中
·target 和 deadends[i] 仅由若干位数字组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/open-the-lock
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这道题目可以选取当前转盘锁数字和目标数字之间的差值作为启发函数,因为转换过程中需要避开会导致转盘锁锁定的数字,因此实际的转换路径一定会比该路径长;同时$H(status)−H(next_status)<=D(status,next_status)$,因此该启发函数一定也是可接纳的。在这种情况下,同一节点只会被加入优先队列一次,并搜索不超过一次,即当我们从优先队列中取出节点x时,$G(x)$一定等于从起点到节点x的「实际」最短路径的长度。
AC代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| struct astar
{
static int geth(const string& status,const string& target)
{
int ret=0;
for(int i=0;i<4;i++)
{
int dist=abs(int(status[i])-int(target[i]));
ret=ret+min(dist,10-dist);
}
return ret;
}
astar(const string& status, const string& target, int g): status_{status}, g_{g}, h_{geth(status, target)} {
f_ = g_ + h_;
}
bool operator< (const astar& that) const {
return f_ > that.f_;
}
string status_;
int f_;
int g_;
int h_;
};
class Solution {
public:
int openLock(vector<string>& deadends, string target) {
int n=deadends.size();
if(target=="0000") return 0;
unordered_set<string> s(deadends.begin(),deadends.end());
if(s.find(target)!=s.end()) return -1;
if(s.find("0000")!=s.end()) return -1;
priority_queue<astar> q;
q.emplace("0000",target,0);
unordered_set<string> hash={"0000"};
while(q.empty()==false)
{
astar x=q.top();
q.pop();
if(x.status_==target) return x.g_;
for(int i=0;i<4;i++)
{
string temp1=x.status_;
string temp2=x.status_;
if(x.status_[i]=='0') temp1[i]='9';
else temp1[i]=temp1[i]-1;
if(x.status_[i]=='9') temp2[i]='0';
else temp2[i]=temp2[i]+1;
if(hash.find(temp1)==hash.end() && s.find(temp1)==s.end())
{
q.emplace(temp1,target,x.g_+1);
hash.insert(temp1);
}
if(hash.find(temp2)==hash.end() && s.find(temp2)==s.end())
{
q.emplace(temp2,target,x.g_+1);
hash.insert(temp2);
}
}
}
return -1;
}
};
|
leetcode 127. 单词接龙[https://leetcode-cn.com/problems/word-ladder/]
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
序列中第一个单词是 beginWord 。
序列中最后一个单词是 endWord 。
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典 wordList 中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]
输出:5
解释:一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。
示例 2:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”]
输出:0
解释:endWord “cog” 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/word-ladder
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
第一次遇到的时候直接cv睡觉了其实和上面这道题类似,只是必须使用在字典中的单词才能转换,因此可以使用当前状态对应的单词和endWord不同的字母数作为启发函数,其一定小于实际的转换路径。同时$H(status)−H(next_status)=[0,1,-1]<=D(status,next_status)$。
这道题的实际难点其实应该是如何选取合适的搜索策略。由于较大的数据范围,使得我们不可能选用遍历所有字典中的单词,将相差单词数为1的两个单词之间建立一条边之中这种时间复杂度为$O(n^2)$的方式来建图。实际上,单词的长度<=10,同时所有的单词均由小写字母构成。可以枚举所有的修改可能,并检查这种修改是否在字典中即可。
AC代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| struct astar
{
static int geth(const string& status,const string& target)
{
int ret=0;
int n=status.size();
for(int i=0;i<n;i++)
{
if(status[i]!=target[i]) ret++;
}
return ret;
}
astar(const string& status, const string& target, int g): status_{status}, g_{g}, h_{geth(status, target)} {
f_ = g_ + h_;
}
bool operator< (const astar& that) const {
return f_ > that.f_;
}
string status_;
int f_;
int g_;
int h_;
};
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
int n=wordList.size();
unordered_set<string> s(wordList.begin(),wordList.end());
priority_queue<astar> q;
q.emplace(beginWord,endWord,0);
unordered_set<string> hash={beginWord};
while(q.empty()==false)
{
astar x=q.top();
q.pop();
if(x.status_==endWord) return x.g_+1;
int t=x.status_.size();
for(int i=0;i<t;i++)
{
for(char j='a';j<='z';j++)
{
if(j==x.status_[i]) continue;
string temp1=x.status_;
temp1[i]=j;
if(hash.find(temp1)==hash.end() && s.find(temp1)!=s.end())
{
q.emplace(temp1,endWord,x.g_+1);
hash.insert(temp1);
}
}
}
}
return 0;
}
};
|
如果直接使用普通的bfs,会造成搜索空间增长过快,即下图所示的情况。在普通的BFS实现中,空间的瓶颈其实主要取决于搜索空间中的最大宽度。
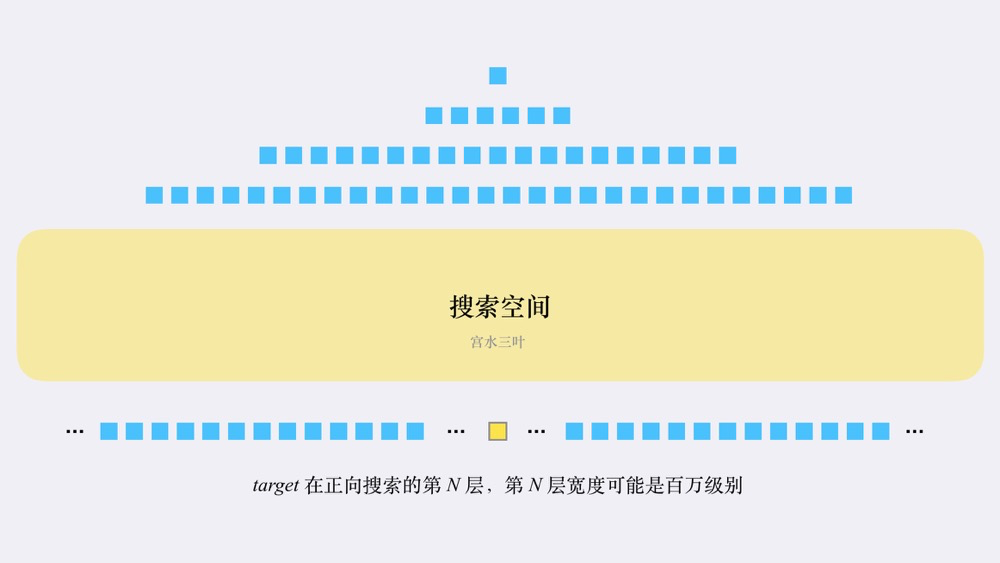
使用双向bfs,同时从两个方向开始搜索,可以很好的解决这一问题。同时从两个方向开始搜索的话,可以快速减少层数,从而解决搜索空间增长过快的问题。具体的运行过程可以总结为:
·创建「两个队列」分别用于两个方向的搜索;
·创建「两个哈希表」用于「解决相同节点重复搜索」和「记录转换次数」;
·为了尽可能让两个搜索方向“平均”,每次从队列中取值进行扩展时,先判断哪个队列容量较少;
·如果在搜索过程中「搜索到对方搜索过的节点」,说明找到了最短路径。
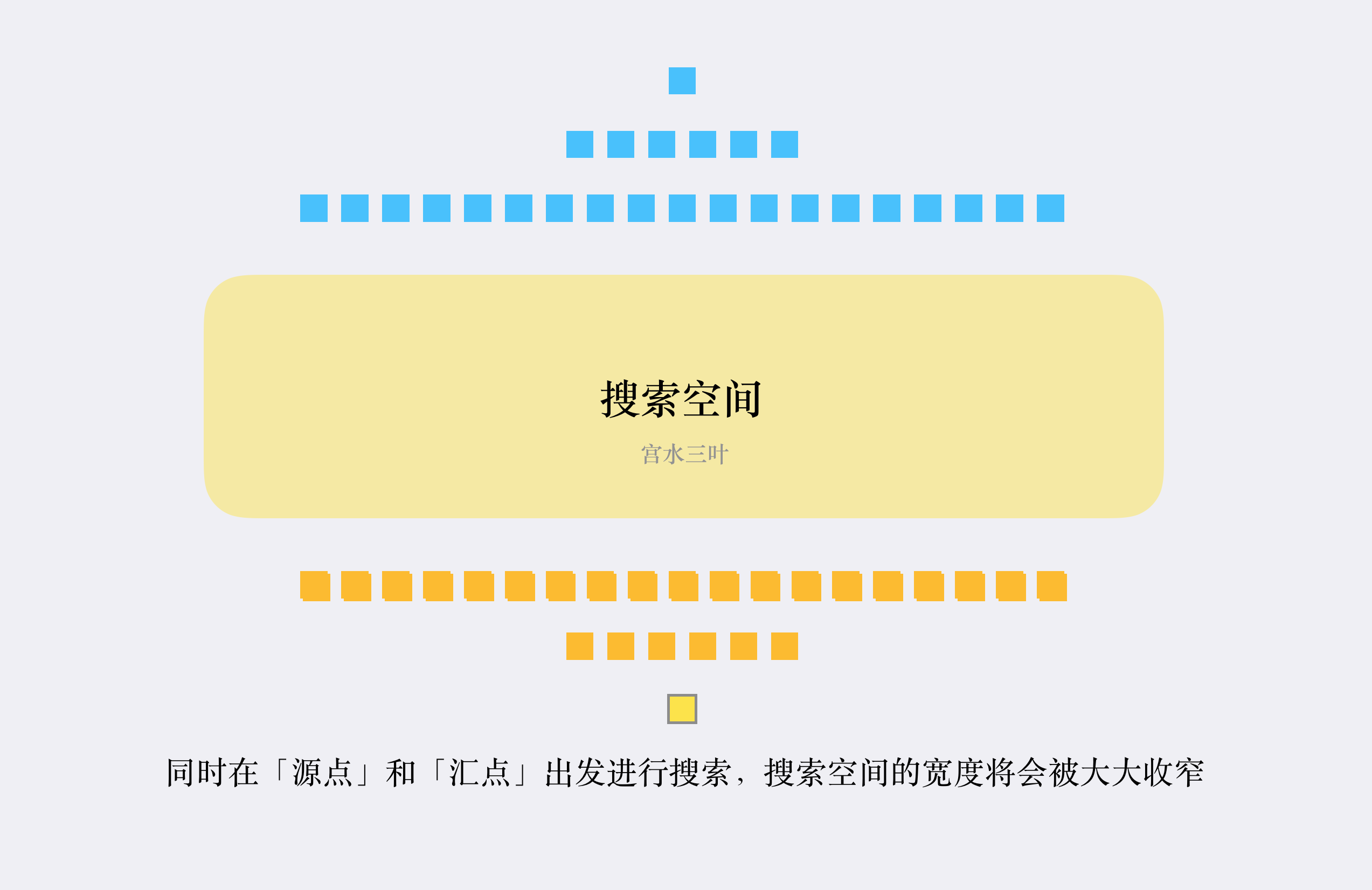
使用双向bfs的AC代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| class Solution {
public:
int bfs(queue<string>& d1,unordered_map<string,int>& hash1,unordered_map<string,int>& hash2,unordered_set<string> &s)
{
int k=d1.size()-1;
for(;k>=0;k--)
{
string x=d1.front();
d1.pop();
int n=x.length();
for(int i=0;i<n;i++)
{
for(int j='a';j<='z';j++)
{
if(x[i]==j) continue;
string temp=x;
temp[i]=j;
if(s.find(temp)!=s.end() && hash2.find(temp)!=hash2.end()) return hash1[x]+hash2[temp];
else if(s.find(temp)!=s.end() && hash1.find(temp)==hash1.end())
{
d1.push(temp);
hash1[temp]=hash1[x]+1;
}
}
}
}
return -1;
}
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_set<string> s(wordList.begin(),wordList.end());
if(s.find(endWord)==s.end()) return 0;
queue<string> d1;
queue<string> d2;
unordered_map<string,int> hash1;
unordered_map<string,int> hash2;
d1.push(beginWord);
hash1[beginWord]=0;
d2.push(endWord);
hash2[endWord]=0;
int ans=-1;
while(d1.empty()==false && d2.empty()==false)
{
if(d1.size()<=d2.size()) ans=bfs(d1,hash1,hash2,s);
else ans=bfs(d2,hash2,hash1,s);
if(ans!=-1) return ans+2;
}
return 0;
}
};
|
需要注意的是,在本题中,for(;k>=0;k--)这一层的循环是必要的,即一定要将该层搜索完毕后,在开始下一层的搜索,否则可能会产生「回头路」,造成结果错误。举例如下图所示,可以通过这组测试样例来观察上述情况产生的原因:
“hbo”
“qbx”
[“abo”,”hco”,”hbw”,”ado”,”abq”,”hcd”,”hcj”,”hww”,”qbq”,”qby”,”qbz”,”qbx”,”qbw”]
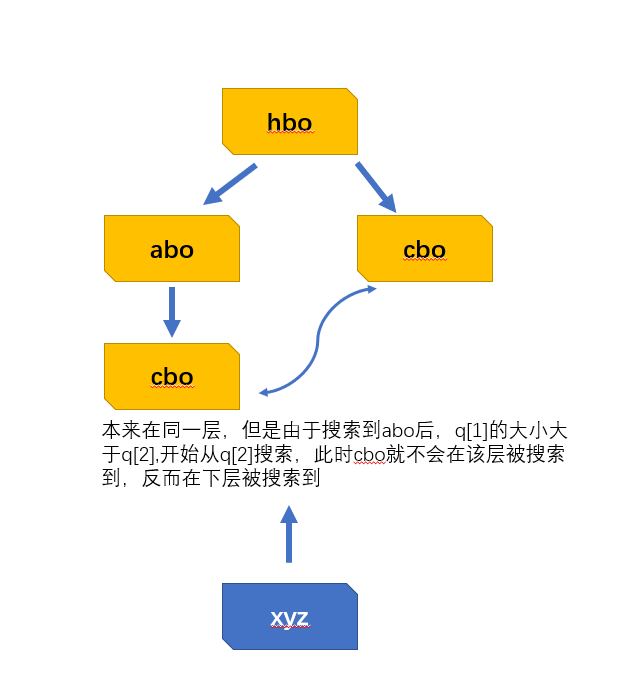
end☆~


