数位dp
数位dp就是套模板 ——lwz
部分内容参考自洛谷日报第84期[https://www.sohu.com/a/273617542_100201031] 以及csdn数位dp总结 之 从入门到模板[https://blog.csdn.net/jk211766/article/details/81474632], 感谢大佬们的文章,把菜鸡如我从谜语人的深渊中拯救出来接下来将通过对模板本身进行分析,以及通过一些例题来了解如何使用模板来解决问题。用的好甚至可以秒切紫题
既然是模板,首先当然要清楚数位dp可以用来解决什么样的问题,总结来说,数位dp可以用于解决在给定区间 [A,B] 内,符合条件 f(i) 的数 i 的个数。条件 f(i) 一般与数的大小无关,而与数的组成有关。如同其名字一样,数位dp便是按照数位来进行dp状态的分析和转移。数位dp解决的问题很多时候都有着人畜无害的外衣,当然更多的外表狰狞甚至直接的暴力方法都仅有O(n)的时间复杂度。但是当这些问题的规模变大,即当n在10^19的级别下,O(n)的时间复杂度就完全无法应对,而数位dp是按位dp,数的大小对复杂度的影响很小,很多情况下能够达到O(log(n))级别,用来解决这样的问题再合适不过了。
从起点向下搜索,到最底层得到方案数,一层一层向上返回答案并累加,最后从搜索起点得到最终答案。这便是数位dp解决问题的过程。而对于 [l,r] 区间问题,我们一般把他转化为两次数位dp,即找 [0,r] 和 [0,l-1] 两段,再将结果相减就得到了我们需要的 [l,r]。
如同大多数dp一般,数位dp有两种实现方式,递推和记忆化搜索。我个人更喜欢记忆化搜索,同时相比递推方式,记忆化搜索更适合作为模板,因此接下来的数位dp的模板以记忆化搜索的形式呈现。
首先我们从这道题开始了解数位dp:万恶之源leetcode 233题[https://leetcode-cn.com/problems/number-of-digit-one/]
题目描述:
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
示例 1:
输入:n = 13
输出:6
示例 2:
输入:n = 0
输出:0
提示:
0 <= n <= 10^9
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-digit-one
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这道题在leetcode上的标签是困难,类似的题在洛谷上的标签是入门。都是红色的233正是10^9的数据范围,使得直接的暴力算法无法达到要求。从这道条件比较简单的题开始,对模板涉及到的内容进行分析。先附上AC代码,并将其作为基础模板:
1 | class Solution { |
从核心的dfs部分开始看。dfs部分dfs(int pos,int sum,int limit)涉及到三个参数,pos,sum以及limit。其中pos表示当前的数位,我们从最高位开始进行dp,sum表示当前状态数码1的个数,是对应这道题目要求而增添的变量,limit表示当前状态是否达到最高位限制。这三个参数中,需要进行解释的主要是limit参数。
一·最高位标记limit
在搜索的数位的过程中,搜索范围可能发生变化。
举个例子:我们在搜索 [0,555] 的数时,显然最高位搜索范围是 0 ~ 5 ,而后面的位数的取值范围会根据上一位发生变化:
·当最高位是 1 ~ 4 时,第二位取值为 [0,9] ;
·当最高位是 5 时,第二位取值为 [0,5] (再往上取就超出右端点范围了)
为了分清这两种情况,我们引入了 limit 标记:
·若当前位 limit=1 而且已经取到了能取到的最高位时,下一位 limit=1 ;
·若当前位 limit=1 但是没有取到能取到的最高位时,下一位 limit=0 ;
·若当前位 limit=0 时,下一位 limit=0 。
1 | int up=9; |
这一部分中的up变量便是表示当前能取到的最高位数,下一位limit的状态自然是i==up && limit。
接下来还有一个需要分析的地方:
1 | if(limit==0 && dp[pos][sum]!=-1) return dp[pos][sum]; |
也就是dp值的保存和取用问题。
举个例子:
假设存在如下约束:数位上不能出现连续的两个1(11、112、211都是不合法的)
假设就是[1,210]这个区间的个数
状态:dp[pos][pre]:当前枚举到pos位,前面一位枚举的是pre(更加前面的位已经合法了),的个数(假设pos从0开始)。
先看错误的方法计数,就是不判limit就是直接记忆化。
那么假设我们第一次枚举了百位是0,显然后面的枚举limit=false,也就是数位上0到9的枚举,然后当我十位枚举了1,此时考虑dp[0][1],就是枚举到个位,前一位是1的个数,显然dp[0][1]=9;(个位只有是1的时候是不满足的),这个状态记录下来,继续dfs,一直到百位枚举了2,十位枚举了1,显然此时递归到了pos=0,pre=1的层,而dp[0][1]的状态已经有了即dp[pos][pre]!=-1;此时程序直接return dp[0][1]了,然而显然是错的,因为此时是有limit的个位只能枚举0,根本没有9个数,状态之间存在冲突。(也可以从上面第一题从数学的角度分析一下,我们记录的是0~9这样的重复状态,而limit==1实际上是属于特殊状态)因此我们可以得到一个结论:当 limit=1 时,不能记录和取用dp值。
类似上述的分析过程,我们也可以得出:当 lead=1 时,也不能记录和取用dp值。(lead用于表示前导零,在后面会讲到,提到时可以翻回来看看)
当然也没有这么绝对,一起都是以实际题目为准。
由此我们发现,模板中需要根据实际情况修改的部分就是下面这一部分:
1 | for(int i=0;i<=up;i++) |
根据实际题目要求,修改其中的约束条件,就可以利用模板来解决问题了。
接下来再看看另一个重要参数,也就是前面提到的lead。
二·前导0标记lead
举个例子:假如我们要从 [0,1000] 找任意相邻两数相等的数
显然 111,222,888 等等是符合题意的数
但是我们发现右端点 1000 是四位数
因此我们搜索的起点是 0000 ,而三位数的记录都是 0111,0222,0888 等等
而这种情况下如果我们直接找相邻位相等则 0000 符合题意而 0111,0222,0888 都不符合题意了
所以我们要加一个前导0标记
·如果当前位 lead=1 而且当前位也是0,那么当前位也是前导0, pos+1 继续搜;
·如果当前位 lead=1 但当前位不是0,则本位作为当前数的最高位, pos+1 继续搜;(注意这次根据题意其他参数可能发生变化)
当然前导 0 有时候是不需要判断的,上述的例子是一个有关数字结构上的性质,0会影响数字的结构,所以必须判断前导0;而如果我们研究的是数字的组成(例如这个数字有多少个 1 之类的问题),0并不影响我们的判断,这样就不需要前导0标记了。
接下来看一个前导零的例子:leetcode 902[https://leetcode-cn.com/problems/numbers-at-most-n-given-digit-set/] 这几个题号都好有梗啊233
题目描述:
我们有一组排序的数字 D,它是 {‘1’,’2’,’3’,’4’,’5’,’6’,’7’,’8’,’9’} 的非空子集。(请注意,’0’ 不包括在内。)
现在,我们用这些数字进行组合写数字,想用多少次就用多少次。例如 D = {‘1’,’3’,’5’},我们可以写出像 ‘13’, ‘551’, ‘1351315’ 这样的数字。
返回可以用 D 中的数字写出的小于或等于 N 的正整数的数目。
示例 1:
输入:D = [“1”,”3”,”5”,”7”], N = 100
输出:20
解释:
可写出的 20 个数字是:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.
示例 2:
输入:D = [“1”,”4”,”9”], N = 1000000000
输出:29523
解释:
我们可以写 3 个一位数字,9 个两位数字,27 个三位数字,
81 个四位数字,243 个五位数字,729 个六位数字,
2187 个七位数字,6561 个八位数字和 19683 个九位数字。
总共,可以使用D中的数字写出 29523 个整数。
提示:
D 是按排序顺序的数字 ‘1’-‘9’ 的子集。
1 <= N <= 10^9
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/numbers-at-most-n-given-digit-set
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
AC代码如下:
1 | class Solution { |
其中
1 | if(lead==1 && i==0) |
便是增加前导零后的处理逻辑的变化,至于具体的要根据实际情况来进行变化。
另外对于状态的记录,最好把所有的额外状态都进行记录,避免状态存在重复和遗漏。虽然这会增加记录数组的维数,但是一般增加的状态都是0,1状态,所以内存方面不会有太多的压力。
数位dp的状态能记录的最好都记录上 ——lwz
附上洛谷制作的搜索步骤的图:
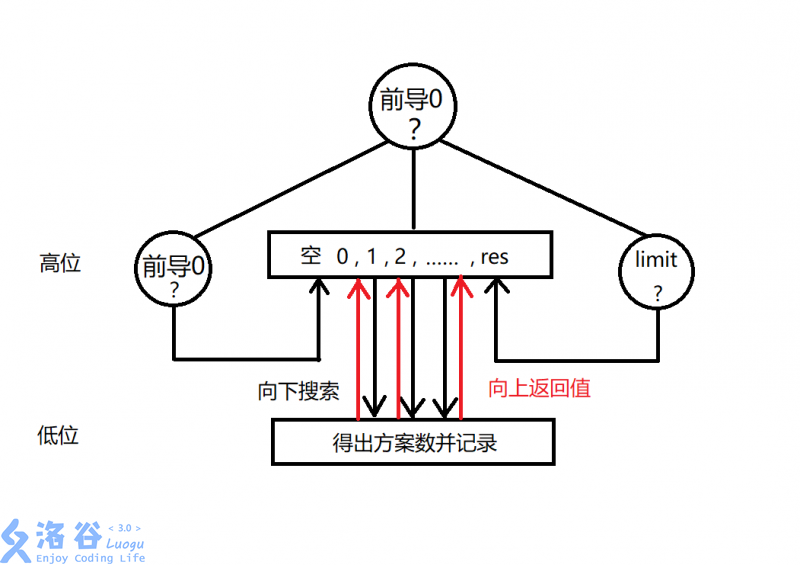
接下来就可以利用模板刷题了,随着使用的次数++,熟练度也会不断++的。数位dp说难也难,说难也不难,通过大量的练习就可以熟练掌握。切紫题指日可待
接下来在来个例子: [HDU3555] [https://acm.hdu.edu.cn/showproblem.php?pid=3555]
题目描述:
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 32756 Accepted Submission(s): 12565
Problem Description
The counter-terrorists found a time bomb in the dust. But this time the terrorists improve on the time bomb. The number sequence of the time bomb counts from 1 to N. If the current number sequence includes the sub-sequence “49”, the power of the blast would add one point.
Now the counter-terrorist knows the number N. They want to know the final points of the power. Can you help them?
Input
The first line of input consists of an integer T (1 <= T <= 10000), indicating the number of test cases. For each test case, there will be an integer N (1 <= N <= 2^63-1) as the description.
The input terminates by end of file marker.
Output
For each test case, output an integer indicating the final points of the power.
Sample Input
3
1
50
500
Sample Output
0
1
15
Hint
From 1 to 500, the numbers that include the sub-sequence “49” are “49”,”149”,”249”,”349”,”449”,”490”,”491”,”492”,”493”,”494”,”495”,”496”,”497”,”498”,”499”,
so the answer is 15.
Author
fatboy_cw@WHU
Source
2010 ACM-ICPC Multi-University Training Contest(12)——Host by WHU
Recommend
zhouzeyong
因为查找的数是一个两位数,所以我们增加pre参数,表示当前数位的前一位,来帮助进行约束判断。AC代码如下:
1 |
|
最后再来道紫题: [luoguP4124] [CQOI2016]手机号码
题目描述:
人们选择手机号码时都希望号码好记、吉利。比如号码中含有几位相邻的相同数字、不含谐音不吉利的数字等。手机运营商在发行新号码时也会考虑这些因素,从号段中选取含有某些特征的号码单独出售。为了便于前期规划,运营商希望开发一个工具来自动统计号段中满足特征的号码数量。
工具需要检测的号码特征有两个:号码中要出现至少 3 个相邻的相同数字;号码中不能同时出现 8 和 4。号码必须同时包含两个特征才满足条件。满足条件的号码例如:13000988721、23333333333、14444101000。而不满足条件的号码例如:1015400080、10010012022。
手机号码一定是 11 位数,前不含前导的 0。工具接收两个数 L 和 R,自动统计出 [L,R] 区间内所有满足条件的号码数量。L 和 R 也是 11 位的手机号码。
输入格式
输入文件内容只有一行,为空格分隔的 2 个正整数 L,R。
输出格式
输出文件内容只有一行,为 1 个整数,表示满足条件的手机号数量。
输入输出样例
输入 #1
12121284000 12121285550
输出 #1
5
说明/提示
样例解释:满足条件的号码: 12121285000、 12121285111、 12121285222、 12121285333、 12121285550。
数据范围:10^10 ≤L≤R<10^11
只需要增加check8,check4,连续段检查三个状态,同时注意前导零的处理就可以了,紫题get√
AC代码如下:
1 |
|
end☆~