前缀和
前缀和是使用一个数组,来储存在当前点之前且包括该点的所有元素的和的一种算法。前缀和算法可以很好的解决一个不变数组的区间查询问题,避免每次查询都需要遍历数组,将查询的时间复杂度降低至O(1)。查询时间复杂度的优化是一个十分常用和重要的问题,而为了解决这些问题,也因此诞生了很多实用的数据结构来解决这些问题。树状数组可以很好的解决存在更新的区间求和问题,而区间最值ST表可以达到O(n)的时间复杂度。区间更新和区间查询问题,则可以通过线段树来很好的解决。线段树以后一定会写的。jpg
对于一维前缀和问题不再赘述,比较简单,下面是LeetCode对应的303题https://leetcode-cn.com/problems/range-sum-query-immutable/ 的AC代码:
1 | class NumArray { |
对于二位前缀和问题,首先要搞明白的是,前缀和储存的是那些点的前缀和,这个问题不像一维前缀和那样直观。接下来介绍的二位前缀和储存的是从(0,0)点到该点的前缀和。
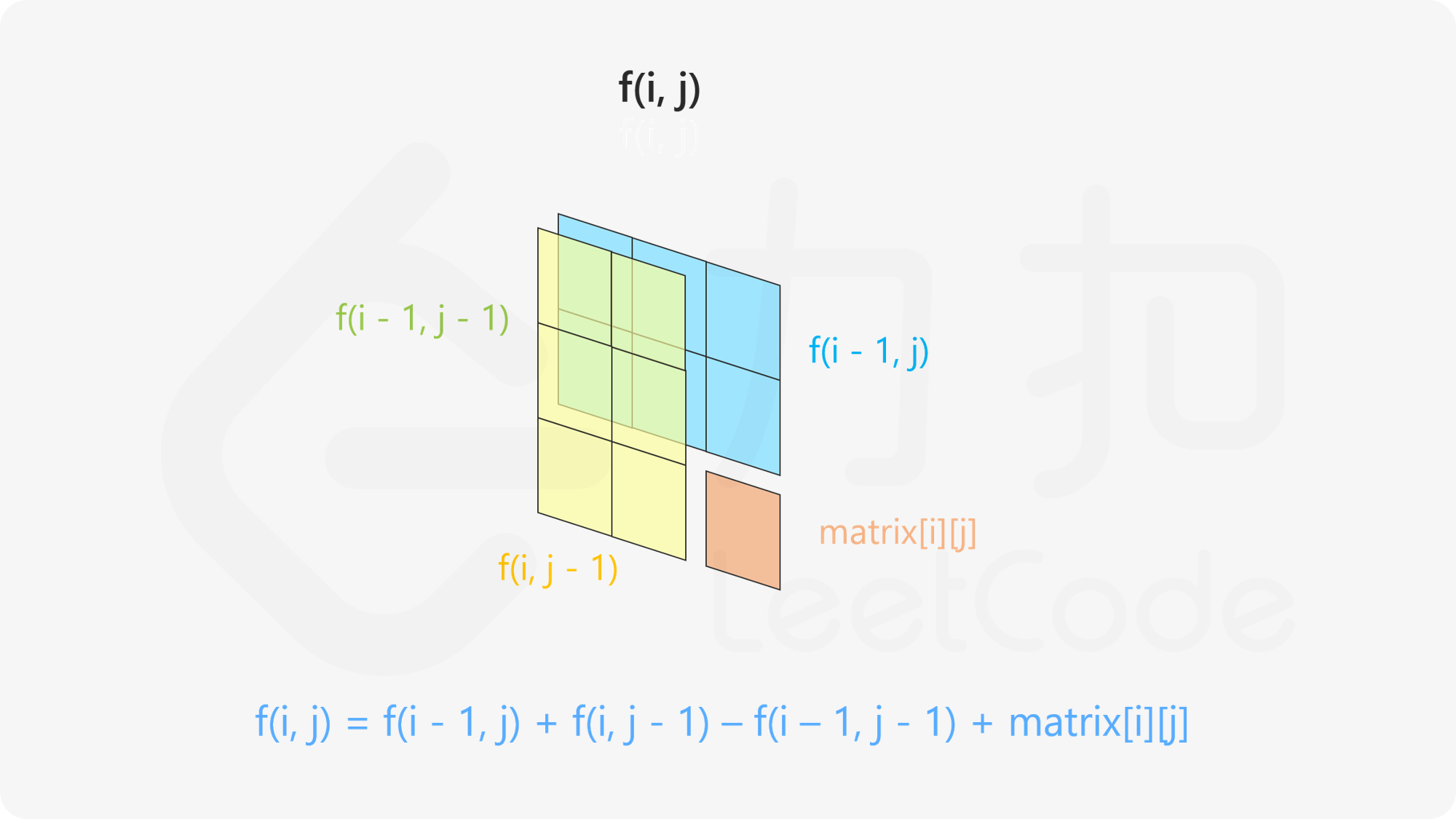
通过上图可以看出,储存的时候实际上一个容斥原理的问题,理解了这一点之后问题就基本解决了。
而在查询的时候,也是一样的原理,只不过是反过来的过程。
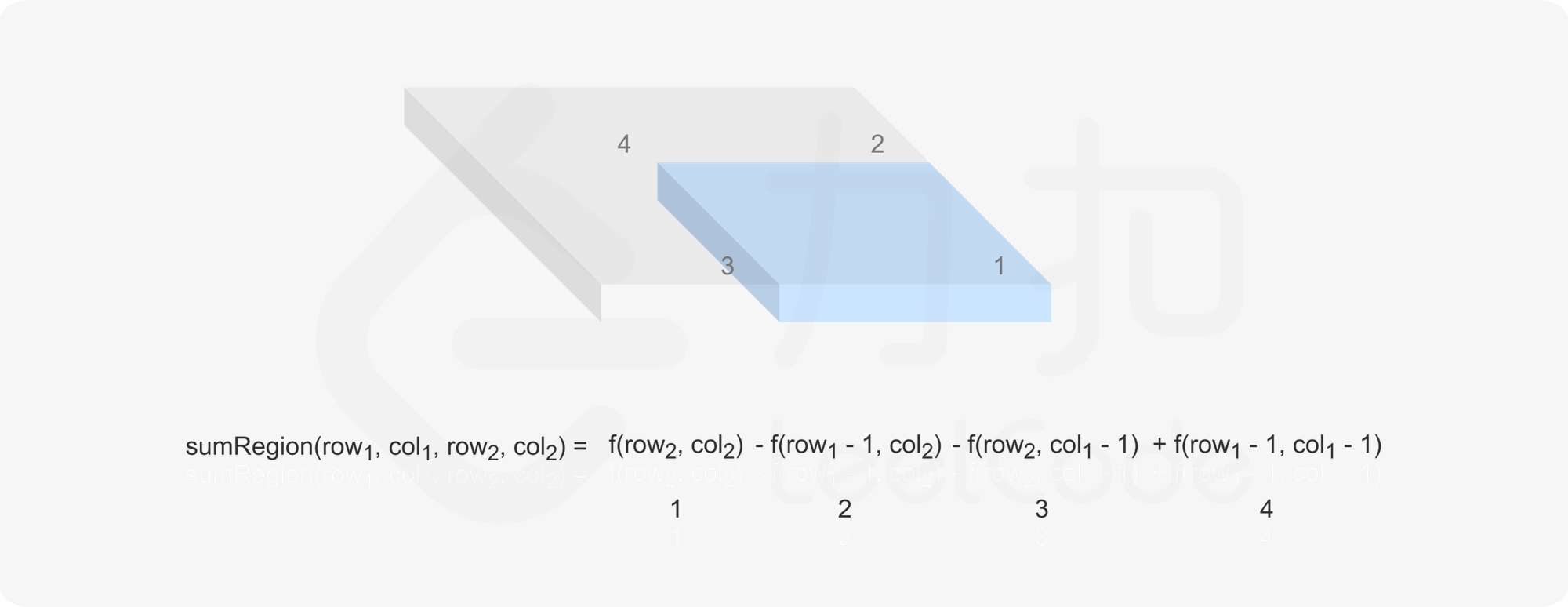
接下来还需要注意一下边界条件的处理。应为在计算的时候,会需要访问到(row1-1,col2)和(row2,col1-1)以及(row1-1,col1-1)这几个点,在row==0 || col==0的条件下会导致溢出。除了单独处理这种情况以外,可以创建一个m+1,n+1大小的二维数组,并将第一行和第一列初始化为0,这样就可以在不影响结果正确性的情况下同时数组的越界访问。
下面的代码时LeetCode对应题目304https://leetcode-cn.com/problems/range-sum-query-2d-immutable/ 的AC实例代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 class NumMatrix {
public:
vector<vector<int>> sums;
int m;
NumMatrix(vector<vector<int>>& matrix) {
m=matrix.size();
if(m==0) return;
int n=matrix[0].size();
sums.resize(m+1,vector<int>(n+1));
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
sums[i+1][j+1]=sums[i][j+1]+sums[i+1][j]-sums[i][j]+matrix[i][j];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
return sums[row2+1][col2+1]-sums[row1][col2+1]-sums[row2+1][col1]+sums[row1][col1];
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/
12 / 12 个通过测试用例
状态:通过
执行用时: 20 ms
内存消耗: 14.9 MB
end☆~