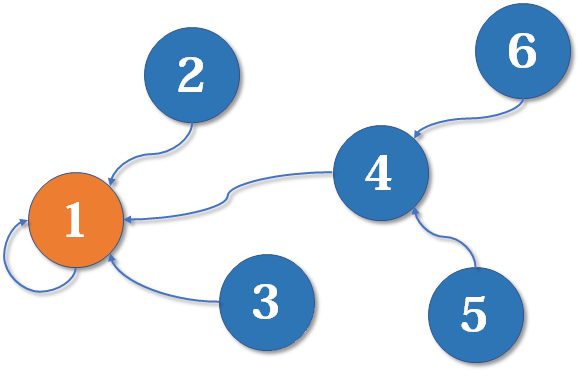
并查集是一种简洁和优雅的数据结构,这一数据结构可以管理一系列不相交的集合,并支持合并和查询两种操作。
并查集实际上是一种树形结构,在并查集中,用一个元素代表整个集合,其方向自下而上,在查询的过程中所有的节点最终都可以找到树的根节点,换言之,就是找到了集合代表的元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 #include <iostream> #include <algorithm> using namespace std;const int maxm=1000005 ;struct node { int x; int y; int d; }; node map[maxm]; int f[maxm];long long ans=0 ;int sum=0 ;bool comp (node x,node y) return x.d<y.d; } int find (int x) if (f[x]==x) return x; f[x]=find (f[x]); return f[x]; } int main () int n,m; cin>>n>>m; for (int i=1 ;i<=n;i++) f[i]=i; for (int i=1 ;i<=m;i++) { int x,y,z; cin>>x>>y>>z; map[i].x=x; map[i].y=y; map[i].d=z; } sort (map+1 ,map+1 +m,comp); for (int i=1 ;i<=m;i++) { int x=find (map[i].x); int y=find (map[i].y); if (x==y) continue ; f[x]=y; ans=ans+map[i].d; sum++; if (sum==n-1 ) break ; } cout<<ans; return 0 ; }
并查集相关的算法问题,大部分都可以将问题转换为图的结构和节点之间的连接问题来进行解决。f[]数组中储存的不一定是该节点对应的最终根节点,也就是说这样构成的并查集不一定是一个只有两层的树结构。https://leetcode-cn.com/problems/couples-holding-hands/]
人和座位用 0 到 2N-1 的整数表示,情侣们按顺序编号,第一对是 (0, 1),第二对是 (2, 3),以此类推,最后一对是 (2N-2, 2N-1)。
这些情侣的初始座位 row[i] 是由最初始坐在第 i 个座位上的人决定的。
示例 1:
输入: row = [0, 2, 1, 3]
输入: row = [3, 2, 0, 1]
len(row) 是偶数且数值在 [4, 60]范围内。
来源:力扣(LeetCode)https://leetcode-cn.com/problems/couples-holding-hands
通过这个例子,可以观察到,最小的交换次数就是情侣对数-1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution {public : vector<int > f; int find (int x) { if (f[x]==x) return x; f[x]=find (f[x]); return f[x]; } int minSwapsCouples (vector<int >& row) int num=row.size (); if (num==0 ) return 0 ; int ans=0 ; vector<pair<int ,int >> map; for (int i=0 ;i<num/2 ;i++) f.push_back (i); for (int i=0 ;i<num-1 ;i=i+2 ) { if (row[i]/2 !=row[i+1 ]/2 ) { map.push_back ({row[i]/2 ,row[i+1 ]/2 }); map.push_back ({row[i+1 ]/2 ,row[i]/2 }); } } int m=map.size (); for (int i=0 ;i<m;i++) { int x=find (map[i].first); int y=find (map[i].second); if (x==y) continue ; f[x]=y; } unordered_map<int ,int > ret; for (int i=0 ;i<num/2 ;i++) { ret[f[i]]++; } for (const auto & [f,sz]:ret) { ans=ans+sz-1 ; } return ans; } };
答案当然是存在问题的。问题的来源正是前面所提到问题,也就是“这种通过遍历所有边来构建并查集的方式建立的并查集,最后f[]数组中储存的不一定是该节点对应的最终根节点,也就是说这样构成的并查集不一定是一个只有两层的树结构。”
1 2 3 4 5 6 输入: [6,2,1,7,4,5,3,8,0,9] 输出: 2 预期: 3
来分析一下。我们可以通过输出f[]数组来看一下并查集得到的结果是什么样的。
可以看到,第三对情侣的根节点结果为1,但情侣1指向了4,只通过对边的一次遍历得到的结果不是一个两层的树的结构,直接通过这一结果来统计联通分量是存在问题的。find(int)函数就可以了,在查找的过程中便会正确更新最终指向的根节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Solution {public : vector<int > f; int find (int x) { if (f[x]==x) return x; f[x]=find (f[x]); return f[x]; } int minSwapsCouples (vector<int >& row) int num=row.size (); if (num==0 ) return 0 ; int ans=0 ; vector<pair<int ,int >> map; for (int i=0 ;i<num/2 ;i++) f.push_back (i); for (int i=0 ;i<num-1 ;i=i+2 ) { if (row[i]/2 !=row[i+1 ]/2 ) { map.push_back ({row[i]/2 ,row[i+1 ]/2 }); map.push_back ({row[i+1 ]/2 ,row[i]/2 }); } } int m=map.size (); for (int i=0 ;i<m;i++) { int x=find (map[i].first); int y=find (map[i].second); if (x==y) continue ; f[x]=y; } unordered_map<int ,int > ret; for (int i=0 ;i<num/2 ;i++) { ret[find (i)]++; } for (const auto & [f,sz]:ret) { ans=ans+sz-1 ; } return ans; } }; 执行用时: 0 ms 内存消耗: 7.1 MB
end☆~